Program for Tower of Hanoi

Tower of Hanoi is a mathematical puzzle where we have three rods and n disks. The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules:
1) Only one disk can be moved at a time.
2) Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack i.e. a disk can only be moved if it is the uppermost disk on a stack.
3) No disk may be placed on top of a smaller disk.

Approach :

Take an example for 2 disks :
Let rod 1 = 'A', rod 2 = 'B', rod 3 = 'C'.

Step 1 : Shift first disk from 'A' to 'B'.
Step 2 : Shift second disk from 'A' to 'C'.
Step 3 : Shift first disk from 'B' to 'C'.

The pattern here is :
Shift 'n-1' disks from 'A' to 'B'.
Shift last disk from 'A' to 'C'.
Shift 'n-1' disks from 'B' to 'C'.

Image illustration for 3 disks :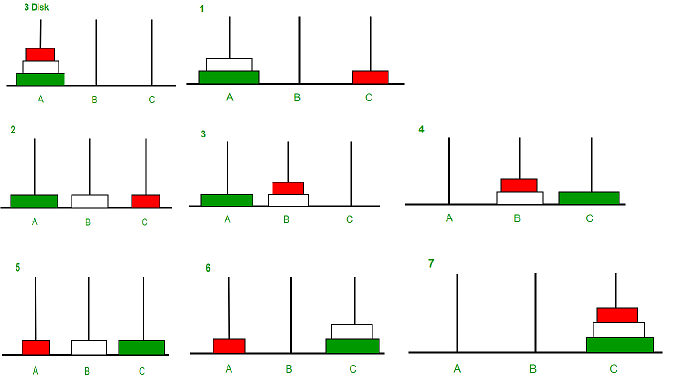

Examples:

Input : 2
Output : Disk 1 moved from A to B
         Disk 2 moved from A to C
         Disk 1 moved from B to C

Input : 3
Output : Disk 1 moved from A to C
         Disk 2 moved from A to B
         Disk 1 moved from C to B
         Disk 3 moved from A to C
         Disk 1 moved from B to A
         Disk 2 moved from B to C
         Disk 1 moved from A to C

Recommended: Please solve it on “PRACTICE ” first, before moving on to the solution.

#include <stdio.h>    // C recursive function to solve tower of hanoi puzzle void towerOfHanoi(int n, char from_rod, char to_rod, char aux_rod) {     if (n == 1)     {         printf("\n Move disk 1 from rod %c to rod %c", from_rod, to_rod);         return;     }     towerOfHanoi(n-1, from_rod, aux_rod, to_rod);     printf("\n Move disk %d from rod %c to rod %c", n, from_rod, to_rod);     towerOfHanoi(n-1, aux_rod, to_rod, from_rod); }    int main() {     int n = 4; // Number of disks     towerOfHanoi(n, 'A', 'C', 'B');  // A, B and C are names of rods     return 0; }

 Move disk 1 from rod A to rod B
 Move disk 2 from rod A to rod C
 Move disk 1 from rod B to rod C
 Move disk 3 from rod A to rod B
 Move disk 1 from rod C to rod A
 Move disk 2 from rod C to rod B
 Move disk 1 from rod A to rod B
 Move disk 4 from rod A to rod C
 Move disk 1 from rod B to rod C
 Move disk 2 from rod B to rod A
 Move disk 1 from rod C to rod A
 Move disk 3 from rod B to rod C
 Move disk 1 from rod A to rod B
 Move disk 2 from rod A to rod C
 Move disk 1 from rod B to rod C

For n disks, total 2n – 1 moves are required.

eg: For 4 disks 24 – 1 = 15 moves are required.

For n disks, total 2n-1 function calls are made.

eg: For 4 disks 24-1 = 8 function calls are made.