What are trees?

• Tree is a hierarchical data structure which stores the information naturally in the form of hierarchy style.
• Tree is one of the most powerful and advanced data structures.
• It is a non-linear data structure compared to arrays, linked lists, stack and queue.
• It represents the nodes connected by edges.

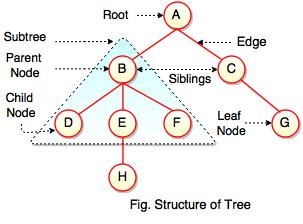
The above figure represents structure of a tree. Tree has 2 subtrees.
A is a parent of B and C.
B is called a child of A and also parent of D, E, F.

Tree is a collection of elements called Nodes, where each node can have arbitrary number of children. 

Field	Description
Root	Root is a special node in a tree. The entire tree is referenced through it. It does not have a parent.
Parent Node	Parent node is an immediate predecessor of a node.
Child Node	All immediate successors of a node are its children.
Siblings	Nodes with the same parent are called Siblings.
Path	Path is a number of successive edges from source node to destination node.
Height of Node	Height of a node represents the number of edges on the longest path between that node and a leaf.
Height of Tree	Height of tree represents the height of its root node.
Depth of Node	Depth of a node represents the number of edges from the tree's root node to the node.
Degree of Node	Degree of a node represents a number of children of a node.
Edge	Edge is a connection between one node to another. It is a line between two nodes or a node and a leaf.

In the above figure, D, F, H, G are leaves. B and C are siblings. Each node excluding a root is connected by a direct edge from exactly one other node 
parent →  children. 

Levels of a node

Levels of a node represents the number of connections between the node and the root. It represents generation of a node. If the root node is at level 0, its next node is at level 1, its grand child is at level 2 and so on. Levels of a node can be shown as follows: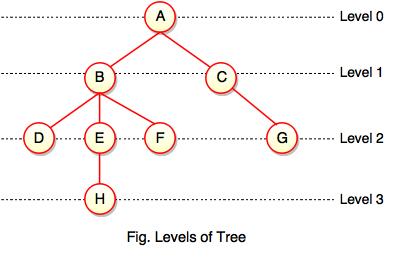



Note: 

- If node has no children, it is called Leaves or External Nodes.

- Nodes which are not leaves, are called Internal Nodes. Internal nodes have at least one child.

- A tree can be empty with no nodes or a tree consists of one node called the Root.

Height of a Node

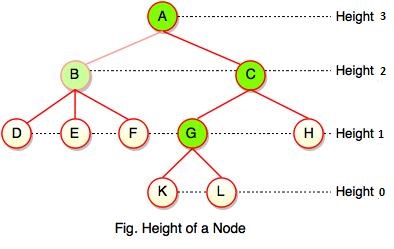
As we studied, height of a node is a number of edges on the longest path between that node and a leaf. Each node has height. 

In the above figure, A, B, C, D can have height. Leaf cannot have height as there will be no path starting from a leaf. Node A's height is the number of edges of the path to K not to D. And its height is 3.

Note: 

- Height of a node defines the longest path from the node to a leaf. 

- Path can only be downward. 

Depth of a Node

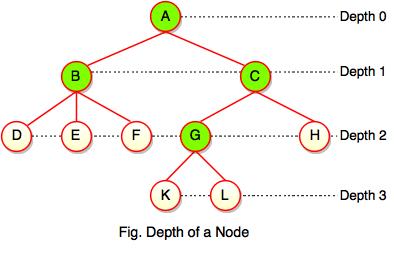
While talking about the height, it locates a node at bottom where for depth, it is located at top which is root level and therefore we call it depth of a node.

In the above figure, Node G's depth is 2. In depth of a node, we just count how many edges between the targeting node & the root and ignoring the directions. 

Note: Depth of the root is 0.

Advantages of Tree

• Tree reflects structural relationships in the data.
• It is used to represent hierarchies.
• It provides an efficient insertion and searching operations.
• Trees are flexible. It allows to move subtrees around with minimum effort